1. 행렬(matrix)의 뜻과 용어
수학에서 행렬이란 수, 문자, 함수를 괄호 안에 직사각형 형태로 배열한 것이다. 이때 각 성분들을 행렬의 원소(element)라 하며, 가로줄을 행(row), 세로줄을 열(column) 이라고 한다. 또한 m행 n열의 원소를 아래첨자를 사용하여 a_m,n 이라 표현한다.

m행 n열을 가진 행렬을 m x n 행렬(m by n matrix) 라고 부르며, m = n 인 경우 정사각행렬 또는 n차 정방행렬(square matrix) 이라고 한다.
또한 원소표기법 a_m,n 으로 나타낼 때 m = n 인 원소들을 행렬의 대각성분이라 부르며 대각성분을 제외한 모든 원소가 0인 행렬을 대각행렬(diagonal matrix) 이라고 부른다. 또한 주대각선 원소들이 모두 1이고 나머지가 0인 정사각행렬을 단위행렬(unit matrix) I 라 부르며 임의의 정사각행렬 A에 대해 IA = AI = A 를 만족한다.
마지막으로, 1개의 행 혹은 1개의 열로만 이루어진 행렬을 벡터로 보아 각각 행벡터 혹은 열벡터로서 보기도 한다.
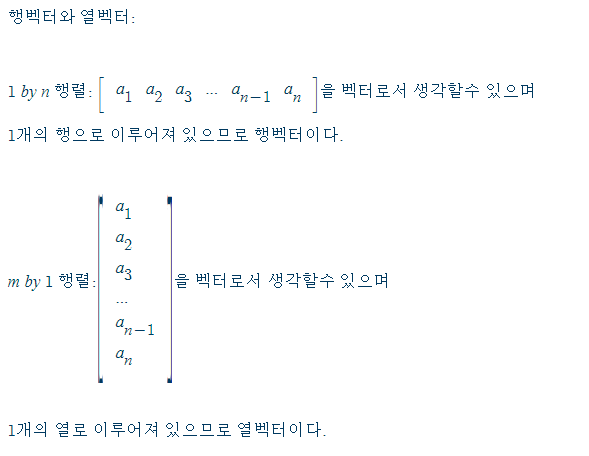
또한 일반적인 m by n 행렬을 행벡터 혹은 열벡터들의 조합으로 생각할수도 있다.
2. 행렬의 기본연산
행렬의 덧셈
행렬끼리의 덧셈은 다음과 같이 정의된다: 행과 열의 개수가 같은 두 행렬 A, B에 대해 그 합 A+B 는 위치가 동일한 각 원소들의 합으로 정의된다.

행렬의 스칼라배
스칼라 c와 행렬 A가 있을 때, 행렬 cA는 A의 각 원소에 c를 곱해준 것과 같다.

행렬의 곱셈
열의 개수와 행의 개수가 같은 두 행렬 A, B가 있을 때 곱 AB 를 정의할수 있고 행렬 AB의 m행 n열 원소는 A의 m번째 행벡터와 B의 n번째 열벡터의 내적과 같다. 또한 AB의 행의 개수는 A의 행의 개수와 같고 열의 개수는 B의 열의 개수와 같다.

행렬의 연산법칙
행렬의 연산에 대해 다음이 성립한다:

'개인공부 > 선형대수학' 카테고리의 다른 글
| 역행렬 (0) | 2021.12.25 |
|---|---|
| 가우스 소거법(2) (0) | 2021.12.24 |
| 가우스 소거법(1) (0) | 2021.12.24 |
| 연립방정식: 가역과 비가역 (0) | 2021.12.24 |
| 교재 정보 (0) | 2021.12.24 |