1. 선형 연립방정식 풀기 - 그림
다음 연립방정식을 살펴보자.

주어진 방정식을 어떻게 풀 것인가? 첫 번째 방정식을 하나의 문자로 정리한 후, 두 번째 방정식에 대입하여 풀 수도 있지만, 이번에는 그래프를 그려 교점을 찾는 방식을 사용해 보자.

붉은색 직선은 x - 2y =1 을 나타내고, 푸른색 직선은 2x + y = 7을 나타낸다.
붉은색 직선의 기울기는 1 / 2 이며, 푸른색 직선의 기울기는 -2 이다. 즉, 각 직선의 개형은 서로 독립적이다.(자기 자신만 고려한다) 이중 연립 방정식의 경우 이런 식의 그림(행 그림 이라고 한다)을 그려서 풀 수도 있지만, 방정식의 미지수가 하나만 추가되어도 두 평면의 교점을 찾아야 하며 그 다음은 두 공간의 교점, 그 다음은 4차원 공간의 교점을 찾아야만 방정식을 풀 수 있다. (못 푼다는 얘기다)
다른 경우로, 각 방정식의 x와 y의 계수들을 벡터로 나타낼수 있다. 아래의 열 그림은 이를 표현한다.
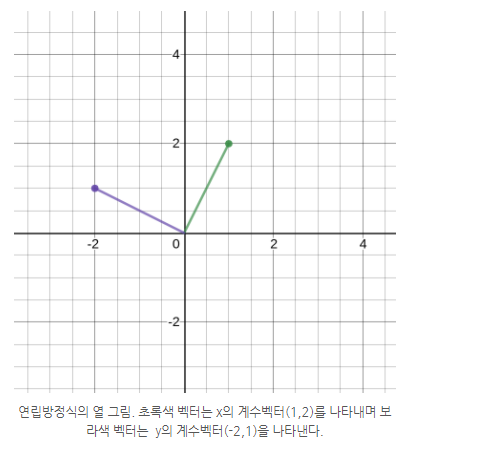
방정식의 해를 찾기 위해 우변의 1, 7 또한 벡터로 나타내어 보면

x의 계수벡터 A = (1,2)의 합과 y의 계수벡터 B = (-2,1)을 올바르게 선형결합하면 (xA + yB) 방정식의 우변을 원소로 가지는 벡터 (1,7)을 얻을 수 있을 것이며 상수쌍 (x, y)는 단 하나만 존재함을 알 수 있다. ("선형" 연립방정식을 풀고 있기 때문이다.)이때 각 계수벡터 A, B 가 서로 독립적임이 중요하다.
선형결합된 벡터에서 상수 x, y 는 각각 3,1 이고 방정식의 해와 일치한다. 이것이 연립방정식을 행렬로 풀어내는 아이디어이다. 행 그림과는 달리 3차원 공간에서도 비교적 쉽게 해를 찾아낼 수 있으며, 그림으로 표현이 불가능한 고차원 공간에서도 간단한 사칙연산을 통해 해를 찾아낼 수 있다. 또한 이를 행렬로 표현할수 있다.
2. 선형 연립방정식 풀기 - 행렬
아까 풀었던 연립방정식을 다시 풀어본다.

주어진 방정식의 행렬 표현은 다음과 같다.

행렬 표현으로 방정식을 어떻게 푸는가? 열 그림으로 방정식을 풀 때 벡터들을 선형결합하여 풀어냈다. 이제 그 벡터들을 계수 행렬의 각 열벡터로 볼 수 있다. 그렇다면 이 과정을 다음과 같이 표현 가능하다:

위에서 얘기한 "연립방정식의 행렬 표현" 을 보면, x성분은 계수행렬의 첫번째 열벡터와, y성분은 계수행렬의 두번째 열벡터와 연산됨을 알 수 있다. 따라서 연립방정식의 행렬 표현이 올바른 풀이를 나타낸다는 것을 알 수 있다.
구체적인 풀이 방법은 다음 포스트 "가우스 소거법" 에서 설명하고 일단 다른거 ㄱㄱ
3. 연립방정식이 유일한 해를 가질 조건: 행렬의 가역성
지금까지 행 그림과 열 그림을 사용하여 연립방정식의 해를 찾는 방법을 알아보았는데, 종종 해를 찾는데 실패할 수 있다. 연립방정식이 해를 가지지 않거나 무한한 해를 가질 때인데, 이때 열 그림이 어떻게 되는지 알아보고, 행렬 표현 방식이 어떻게 되는지 공부한다. 다음 연립방정식은 각각 해를 가지지 않고(첫번째) 무한한 해(두번째)를 가진다. 예시를 들기 위해 두 연립방정식을 준비했다. 첫 번째 연립방정식은 해를 가지지 않고, 두 번째 연립방정식은 무한한 해를 가진다.
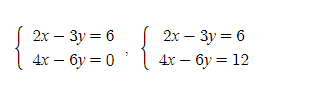
두 연립방정식의 열 그림을 그려보면:

계수행렬의 열벡터들(그림에서 R, B)을 임의로 선형결합하여(aR + bB) 구하고자 하는 연립방정식의 우변 열벡터(각각 Y, G)를 얻는 상수 계수(a, b)를 찾아서 풀었다. 이제 두 가지 연립방정식에 대해 열 그림을 해석해 보면 다음과 같다.
첫 번째 방정식: 연립방정식이 무한한 해를 가질 때
선형결합 aR + bB를 벡터 Y와 일치하게 하는 경우의 수는 무한개이다. 세 가지 벡터가 동일 직선상에 위치하므로 직관적으로 무한한 방법을 가지는 것을 알 수 있다.따라서 첫 번째 연립방정식에 대해 상수쌍 (a, b)를 얻는 방법은 무한히 많다. 즉 무한한 해를 가진다.
두 번째 방정식: 연립방정식이 해를 가지지 않을 때
이제 두 번째 방정식으로 가보자. 선형결합 aR + bB를 벡터 G와 일치하게 하는 경우의 수는 존재하지 않는다. 벡터 R, B가 동일 직선상에 위치하므로 모든 선형결합 aR + bB또한 해당 직선상에 위치한다. 벡터 G가 해당 직선 바깥에 존재하므로, aR + bB = G 를 만족하는 상수쌍(a, b)는 존재하지 않는다. 즉 해가 존재하지 않는다.
결론: 연립방정식이 유일한 해를 가질때 계수행렬의 열들은 서로 독립이다. 이때 계수행렬이 가역(invertible)이라고 한다.
위에서 살펴본 두 가지 경우에 대해 공통점을 찾을 수 있다. 바로 계수행렬의 두 개 이상의 열벡터들이 동일 직선상에 위치, 즉 종속적이다. 이때 선형 연립방정식은 유일한 해를 가지지 않으며, 계수행렬은 비가역 행렬(singular matrix) 이라고 한다.
그 반대의 경우, 즉 행렬의 모든 열벡터들이 서로 독립일 때 해당 연립방정식은 유일한 해를 가진다. 이때 계수행렬을 가역 행렬(invertible matrix) 이라고 한다.
또한 해를 찾거나 존재하지 않음을 보일 수 있는 연립방정식의 계수 행렬들은 정사각행렬일 것이므로, 가역 행렬은 무조건 정사각행렬이며 행렬의 가역과 비가역을 판단하려면 행렬이 정사각행렬이라는 전제가 필요함을 알 수 있다.
4. 요약: 가역 행렬과 비가역 행렬(1)

연습 문제
(4.1절 연습문제 03번)주어진 연립방정식에서 첫 번째 행의 방정식이 두 번째 행의 방정식에 더해진다면 어떤 것이 바뀌는가? 각각의 경우에 대하여 답하라: 행 그림의 평면, 열 그림의 벡터, 계수 행렬, 해


(4.1절 연습문제 29번)u와 v가 3X3 행렬 A의 처음 두 열 이라고 하자. 행렬을 비가역 행렬로 만드는 세 번째 열 w는 무엇인가? 비가역인 경우에 Ax = b 의 일반적인 열 그림과 행 그림을 설명하라.(단 b는 임의의 열벡터)

'개인공부 > 선형대수학' 카테고리의 다른 글
| 역행렬 (0) | 2021.12.25 |
|---|---|
| 가우스 소거법(2) (0) | 2021.12.24 |
| 가우스 소거법(1) (0) | 2021.12.24 |
| 행렬 기본 (0) | 2021.12.24 |
| 교재 정보 (0) | 2021.12.24 |