1. 가우스 소거법이 올바른 해를 주는 이유 - 소거법의 행렬 표현
저번 포스트에서 공부한 가우스 소거법을 요약해 보자면 다음과 같다.

행 교환과 소거등 가우스 소거법의 일련의 과정이 정확히 어떠한 원리로 작동하는 것이고, 맞는 해를 주는 이유에 대한 정확한 입증을 위해 행렬의 곱셈을 사용한다. 행 교환과 원소 소거는 행렬방정식의 양변에 특정한 행렬을 곱하는 것으로 설명 가능하다.
소거 행렬
먼저 원소 소거부터 알아보자. 계수 행렬에서 특정한 원소를 소거하기 위해 우리는 다른 행에 적절한 상수를 곱한 후 소거하고자 하는 원소가 있는 행에 더해주었다. 이때 우변 열벡터 또한 동일한 과정을 거쳐주어야 하는데, 해 벡터 (x, y, z...) 에는 그러한 과정을 가하지 않았다. 그 이유를 설명하기 위해, 소거 행렬(elimination matrix)을 도입한다.

예시를 들기 위해 아무 3차 연립방정식이나 풀어본다:
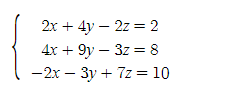
방정식의 양변에 소거 행렬을 곱해 계수 행렬의 2행 1열을 소거할것이다.

소거 행렬과 가우스 소거법의 소거 과정이 올바르다는 것을 알았다. 이제 소거 행렬을 어떻게 찾는지를 알아본다.
n차 정방행렬의 x행에 상수 c를 곱한 후 y행에 더해주어 소거하는 행렬을 찾아야 하는데, 이를 찾기 위해 행렬 곱셈 매커니즘을 알아야 한다. 행렬곱 EA 에서 y행 성분들은 E의 y행에 A의 모든 열들을 내적하여 나타난다. 그러므로 소거 행렬 E의 y행 n열 성분은 A의 n행에 작용하여 그 값들을 A의 y행 성분들에 더해준다. 이러한 이유로 인해 단위행렬은 주대각선이 1, 다른 원소들이 0인 행렬인 것이다. (행렬곱 IA = A 가 되려면 단위행렬의 y행이 A의 y행에만 작용하고 나머지를 0을 만들어야 하므로 y행의 y열 성분이 1이고 나머지는 0인 것)
이러한 원리를 사용해 원하는 소거를 작용시키는 소거 행렬을 찾을 수 있다. n차 정방행렬의 x행에 상수 c를 곱한 후 y행에 더해주어 소거하는 행렬 P는 다음과 같다:

치환 행렬
행 교환 과정 또한 행렬표현이 가능하다. 임의의 행렬 A의 행을 교환해주는 행렬을 치환 행렬(permutation matrix) 이라고 하며 P로 표기한다:

소거 행렬과 마찬가지로 치환 행렬 또한 방정식 Ax = b 의 양변에 곱해주어 행 교환을 할 수 있다. 따라서 x에는 영향을 주지 않고 A와 b에만 영향을 주는 것이다.
이제 치환 행렬을 찾는 방법을 알아보자. n차 정방행렬의 m행과 n행을 바꿔주는 행렬 P을 찾기 위해 소거 행렬과 마찬가지로 행렬 곱셈 매커니즘을 살펴보면 된다. 등식 IA = A 로 시작하자. 여기서 A는 n차 정방행렬이고 I는 단위행렬이다.

좌변의 k행 성분들은 I의 k행에 A의 모든 열들을 내적하여 나타난다. I의 k행 원소들은 k열 원소가 1이고 나머지 원소들이 0이므로 결국 A 각 열들의 k행 성분들만 남기게 되고, 결과적으로 모든 행들이 기존 행렬과 똑같이 나온다.
이것을 사용하면 치환 행렬이 어떠한 원소들을 가지는지 볼 수 있다. 행렬곱 PA의 k행을 A의 m행으로 나타내고 싶으면, 행렬 P의 k행 원소 중 m열 원소를 1로 만들고 나머지 원소를 0으로 만들면 된다. 따라서 행 p와 q를 바꾸는 치환행렬은 다음과 같다:

연습 문제
(4.2절 연습문제 30번)임의의 정방행렬 A를 위삼각 행렬 U로 행 교환 없이 소거를 진행했다고 하자. 이때 U의 i행은 A의 어떤 행들의 선형결합인가? 다음 명제의 참 거짓을 판단하라: Av = 0 이면 Uv = 0 인가? Av = b 이면 Uv = b 인가? (단 b는 영행렬이 아니다)

(4.2절 연습문제 31번)100개의 미지수 v = (v1, v2, v3...v100) 에 대해 100개의 연립방정식을 나타내는 Av = 0 으로 시작하자. 소거법을 통해 계수행렬 A의 마지막 행이 0으로 줄어든다고 하자. 따라서 마지막 방정식은 0 = 0 이고 시스템은 비가역이다.
다음 물음에 답하라: (1)주어진 시스템에서 임의의 100개의 행들의 선형결합은 무엇인가? (2)해당 시스템은 무수히 많은 해를 가진다. 이때 100개의 열들의 선형결합은 무엇인가? (3)0을 성분으로 가지지 않는 100차 정방행렬을 만들어라. 그 행렬에 대해 Av = 0의 행 그림과 열 그림을 말로 설명하라.

'개인공부 > 선형대수학' 카테고리의 다른 글
| 대칭행렬/차분행렬 (0) | 2021.12.25 |
|---|---|
| 역행렬 (0) | 2021.12.25 |
| 가우스 소거법(1) (0) | 2021.12.24 |
| 연립방정식: 가역과 비가역 (0) | 2021.12.24 |
| 행렬 기본 (0) | 2021.12.24 |