1. 직교 행렬
정규직교 행렬(standard orthogonal matrix) 혹은 직교 행렬은 행렬의 전치가 역행렬과 같은 정사각행렬이다. 즉 A^T = A^-1 이다.

여기서 한 가지 성질을 확인할 수 있다. 행렬이 정규직교행렬일 때 행렬의 모든 열벡터의 크기는 1이며 서로 직교한다. (내적값이 0이다.) 일반적인 경우에 대해 증명은 다음과 같다:

또한 직교 행렬과 다른 직교 행렬의 곱이 존재한다면 그 곱 또한 직교 행렬이다. 즉 두 직교행렬 Q_1, Q_2 에 대해 Q = Q_1 Q_2 또한 직교 행렬이다.

(참고)행렬이 정사각행렬이 아닐지라도 열벡터들의 길이가 1이고 서로 직교하면 Q^T Q = I 를 만족할 수 있다. 다만 이 경우 행렬 Q의 열의 개수가 행의 개수보다 많아야 하며(즉 Q가 m x n 행렬일 때 m > n), 정규직교행렬 Q의 경우 Q^T Q = QQ^T = I 를 만족하지만 직사각행렬의 경우 Q^T Q = I를 만족하더라도 QQ^T =/= I 이다. 즉 이 경우 Q^T 는 Q의 왼쪽 역행렬이다.(=왼쪽에서 곱해주어야만 단위 행렬을 얻는다.)
2. 직교좌표계에서 벡터의 회전
직교 행렬의 기하학적인 의미를 알아본다. 직교 행렬의 특성 두 가지가 있다. 하나는 직교행렬의 모든 열벡터들의 길이가 1이라는 것이며 두 번째는 그 열벡터들은 서로 직교한다는 것이다. 즉 직교행렬의 열들은 특정 직교좌표계의 단위벡터들이다. 예를 들어 흔히 알고 있는 3차원 좌표계의 세 가지 단위벡터들은 i = (1,0,0), j = (0,1,0), k = (0,0,1) 이고 이는 직교행렬 Q = (i, j, k)= I 의 열들이다.
이 특성을 사용하여 직교좌표계에서 특정 벡터를 회전된 좌표계의 좌표로 표현 가능하다. (=벡터 회전이 가능하다.)
이해를 쉽게 하기 위해 2차원 평면좌표계로 예를 들어보면 다음과 같다:


+벡터에 곱해준 행렬 R의 열들의 크기가 모두 1이므로 원래 벡터b 의 길이가 유지되며 방향만 바뀐 것을 알 수 있다. 만약 벡터의 크기또한 바구고 싶다면 R에 알맞은 스칼라배를 해 주면 된다.
3. 대칭직교 행렬
대부분의 행렬은 대칭이면 직교가 아니고 그 반대의 경우도 마찬가지이다. 다만 대칭직교 행렬의 경우 대칭이면서 동시에 직교이다. 이러한 것이 어떠한 조건 하에 성립하는지, 성립한다면 그 행렬은 어떠한 특성을 가지는지 알아본다.
예시로 1과 -1 을 교차하며 원소로 가지고 -1 로 끝나는 대각행렬 D를 생각해보자.
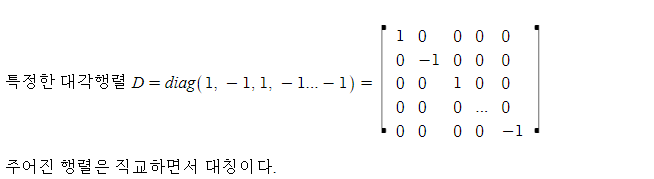
위의 대각행렬 D와 적당한 직교행렬 Q를 사용하여 대칭직교 행렬 QDQ^T 를 만들 수 있다. 또한 모든 대칭직교 행렬은 QDQ^T 꼴로 표현이 가능하다.(이에 대한 자세한 설명은 벡터의 고유값 파트에서 배운다.)

(4.5절 연습문제 20-a)Q가 직교 행렬이라고 하자. Q의 역행렬 또한 직교 행렬인 이유는 무엇인가?

(4.5절 연습문제 22번)u가 단위 열벡터일때 행렬 H = I - 2uu^T 가 대칭직교 행렬임을 보여라.



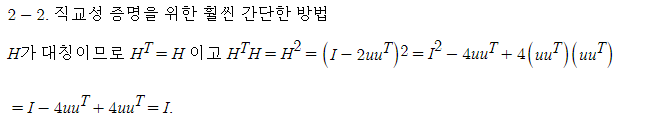
'개인공부 > 선형대수학' 카테고리의 다른 글
| 행렬의 영공간 (0) | 2021.12.25 |
|---|---|
| 벡터공간,부분공간, 행렬의 열공간 (0) | 2021.12.25 |
| 대칭행렬/차분행렬 (0) | 2021.12.25 |
| 역행렬 (0) | 2021.12.25 |
| 가우스 소거법(2) (0) | 2021.12.24 |