코로나 때문에 격리 및 싸지방 통제+전역후 싸돌아다니기 및 GTA로 인해 간만에 쓰는 포스트
이번 포스트에서는 지금껏 공부한 영공간 및 열공간에 전치행렬 A^T를 추가하여 A^T의 열공간과 영공간, 그리고 이 네 가지 부분공간들간의 관계를 알아본 후 선형대수학의 기본정리 첫 번째를 공부한다.
1. 행공간 = 전치 행렬의 열공간
임의의 행렬 A를 생각한다. 보기 편하도록 적당한 숫자를 넣어 3X5 행렬을 만들면

여기서 행렬 A의 열공간과 영공간은 바로 찾을 수 있다. 이제 새로운 부분공간을 공부한다. 첫번째로 A의 행들의 선형결합으로 생성되는 부분공간을 행공간(row space)라 하고 기호로 C(A^T)로 표시한다. 기호를 살펴보면 행공간은 원래 행렬을 전치시켜서 얻은 행렬의 열공간과 같은데, (당연한 얘기지만)이는 행렬을 전치할 때 행과 열이 바뀌기 때문이다. 또한 주어진 행렬의 행공간은 R^5 상의 2차원 평면일 것이다.

행공간의 기저는 주어진 행렬에서 피봇을 포함하고 있는 행벡터들이다. 이때 필자가 C(A^T)의 기저를 A의 행벡터가 아닌 완전히 소거된 행렬 RREF의 피봇 행벡터들로 구성한 것을 볼 수 있다. 행렬의 소거 과정이 행들의 선형결합이며, 행공간 생성 또한 행들의 선형결합으로 이루어지기 때문에 소거된 행렬에서 기저를 찾아도 무방한 것이다. 즉 A의 소거 R에 대해 C(A^T) = C(R^T) 이다.

2. 좌영공간 = 전치 행렬의 영공간
이제 전치행렬의 영공간에 대해 살펴보자. 좌영공간(left nullspace)이라고 하며, 기호로 N(A^T)로 표시한다. 행공간을 설명할 때 사용한 행렬 A를 계속 사용해서 보면

행렬을 전치시킨 후 그 행렬의 영공간을 찾아주면 된다.

행렬을 소거하여 사다리꼴 혹은 기약행 사다리꼴로 만들었을 때 행렬의 좌영공간이 유지될까? 즉 N(A^T) = N(R^T) 인가? 유지되지 않는다 이다. 행렬 A로 반례를 들 수 있다.

물론 특수한 행렬의 경우 원래 행렬의 좌영공간과 소거된 행렬의 좌영공간이 같을 수 있다. 다음과 같이 기억하면 된다.

이번에 배운 행공간 및 좌영공간 그리고 열공간과 영공간 네 가지를 "네 가지 기본 부분공간"이라고 칭하며 방정식 Av = b와 벡터공간을 공부할때 많이 나온다고 한다.
3. 정리: 소거된 행렬과 부분공간
행공간과 좌영공간에 대해 알아보았고, 이제 나머지 두 부분공간인 열공간과 영공간에 대해 알아보자. 이미 학습한 내용이므로 정의 같은 건 건너뛰고 소거시 공간이 유지되는지만 판단한다.
먼저 열공간 C(A)에 대해 알아보자. A를 R로 소거하였을 때 열공간은 유지되지 않는다. 간단하게 생각해보면, 연립방정식을 행렬 꼴로 표현하여 풀 때(Av = b 꼴로 풀 때) 가우스 소거법을 사용하여 좌변 A를 소거하여 풀어주는데, 이때 우변의 벡터 b 또한 동일한 소거를 거쳐야 한다. 따라서 열공간은 일반적으로 보존되지 않는다.
이제 영공간에 대해 판단해보자. 방법은 열공간 판단시와 같은데, 방정식 Av = 0 과 Rv = 0을 비교해보면 된다. 이는 단순히 모든 상수항이 0인 연립방정식을 푸는 것인데, 소거를 한다고 해서 우변의 영벡터가 바뀌지 않으며 영공간 해가 유지되므로 행렬 소거시 영공간은 보존된다. 지금까지 공부한 내용을 정리해 보면 다음과 같다:
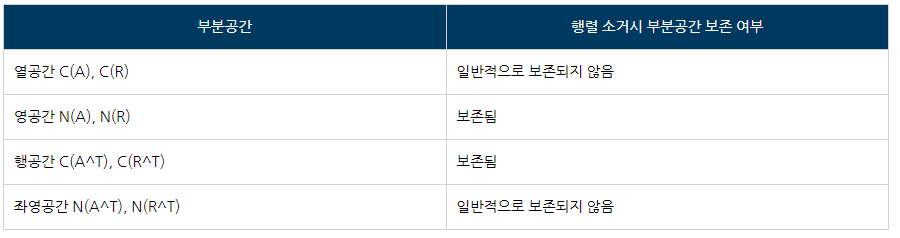
4. 방정식 Av = b 의 기본 부분공간에 대한 그림
지금껏 우리가 행렬에 관해 배운 부분공간은 총 4가지로, 열공간, 영공간, 행공간, 좌영공간이다. 언급했듯이 이 네 개의 부분공간은 방정식 Av = b 에서 서로 연관되어 있으며 그림으로 나타내면 다음과 같다.

지금부터 이 포스트에서 이야기한 모든 내용들이 이 그림에 전부 표현되어 있다. 밑에서 설명하는 모든 내용들은 다음과 같은 전제조건이 필요하다: 그림에서 나오는 행렬 A는 mXn 행렬이고 rank(A) = r 이다.
우선 왼쪽 부분인 행공간과 열공간부터 보자.
4.1. 행공간과 영공간 rowspace and nullspace
그림을 살펴보면 여러 가지 정보들이 나와 있는데, 우선 행공간과 영공간이 위치하는 왼쪽 부분에 R^n 이라고 쓰여져 있는게 보일 것이다. A가 mXn 행렬이므로 C(A^T)와 N(A)는 R^n 상의 부분공간이다. 두 번째로 rank(A) = r 이므로 행공간의 차원은 r임이 분명하다. 세 번째로 영공간의 차원을 보자. 행렬 A가 n개의 열을 가지고 r개의 피봇 열을 가지므로 자유 변수는 n - r개이며 이는 영공간의 치원과 같다. 즉 dim N(A) = n - r 이다. 네 번째로 dim C(A^T) + dim N(A) = r + n - r = n 이다.
아래는 위 내용을 정리한 것이다.
4-1-1. C(A^T)와 N(A)는 R^n 상의 부분공간이다.
A가 mXn 행렬이므로 이는 당연한 사실이다.
4-1-2. dim C(A^T) = r 이고 dim N(A) = n - r 이다.
rank(A) = r 이므로 dim C(A^T) = r 이며, A가 n개의 열을 가지고 r개의 피봇 열이 존재하므로 A에 n - r 개의 자유 열이 존재한다. 따라서 dim N(A) = n - r 이다.
4-1-3. dim C(A^T) + dim N(A) = r + n - r = n 이다.
당연한 얘기지만 동일한 행렬에 대해 행공간의 차원과 영공간의 차원을 더하면 무조건 열의 개수와 같다는 것을 기억해 두자.
4-1-4. 동일한 행렬에 대해 행공간과 영공간은 서로 수직이다.
행공간에 속한 임의의 벡터와 영공간에 속한 임의의 벡터를 내적한 것이 항상 0이라고 이해하면 될것이다. 이때 정의되지 않는 변수는 0으로 계산한다. 증명은 아래와 같다:

4-1-5. 방정식 Av = b의 특수해는 행공간에 존재한다.
지금 당장은 명확한 이유를 설명해 줄 순 없으니 일단 인정하고 넘어가도록 하자. 다음 포스트에서 설명할 것이다.
4-1-6. 방정식 Av = 0의 해는 영공간에 존재한다.
영공간 자체가 영공간 해들의 집합이므로 당연한 이야기이다.
R^n 상의 두 기본 부분공간인 행공간과 영공간에 대한 중요한 특성들을 알아보았으니, 이번에는 그림의 오른쪽에 위치한 R^m 상의 열공간과 좌영공간을 다루어 보자.
4.2. 열공간과 좌영공간 columnspace and left-nullspace
여기서 얻을 수 있는 정보들은 바로 이전 절에서 얻은 정보들과 비슷하다. 행렬 A가 mXn 행렬이므로 열공간은 R^m 상의 부분공간임이 확실하고 좌영공간 또한 그러하다. dim(C(A^T)) = r 이라고 가정했으므로 dim(C(A^T)) = 1 또한 성립한다. nXm행렬 A^T의 피봇 열 개수가 r개이므로, 이 행렬의 영공간인 A의 좌영공간 N(A^T)의 차원은 m - r 이다. 아까와 마찬가지로 아래에 열공간과 좌영공간에 대해 알아야 할 특성들을 정리해 놓았다.
4-2-1. C(A)와 N(A^T)는 R^m 상의 부분공간이다.
A가 mXn 행렬이므로 참이다.
4-2-2. dimC(A) = r 이고 dimN(A^T) = m -r 이다.
rank(A) = r 이므로 열공간의 차원 또한 r이고 A가 nXm 행렬, 피봇 열이 r개이므로 좌영공간의 차원은 m - r 이다.
4-2-3. dimC(A) + dimN(A^T) = r + m - r = m 이다.
2-2에 의해 참이며, 항상 성립한다는 것을 기억하자.
4-2-4. 동일한 행렬에 대해 열공간과 좌영공간은 서로 수직이다.
1-4와 동일한 방법으로 증명이 가능하다. A 대신 A^T를 넣어 증명해 보자. 과정생략.
4-2-5. 방정식 Av = b에서 v가 존재한다면 우변의 벡터 b는 열공간에 존재해야 하며 그 역 또한 성립한다.
행렬-벡터 곱 Av는 A의 각 열들을 v의 성분만큼 선형결합해서 얻어진다. Av와 동일한 b가 존재하려면 열들의 선형결합으로 이루어진 부분공간 C(A)에 b가 존재햐여야 한다.
4-2-6. 방정식 A^T v = 0의 해는 좌영공간에 존재한다.
좌영공간이 A^T의 영공간이므로 참이다.
5. 선형대수학의 기본정리 1
(4-)1-2, 1-3, 2-2, 2-3은 선형대수학의 첫 번째 기본정리이다.

'개인공부 > 선형대수학' 카테고리의 다른 글
| 행렬식 (0) | 2021.12.25 |
|---|---|
| 선형대수의 기본정리 (2) (0) | 2021.12.25 |
| 벡터공간의 기저와 차원 (0) | 2021.12.25 |
| Av=b의 완전해 구하기 (0) | 2021.12.25 |
| 행렬의 영공간 (0) | 2021.12.25 |