이전에 공부한 Repetition code의 경우 diversity 관점에서 충분한 성능을 보여주지만(에러 발생 확률 낮음) 전송하는 symbol이 최대의 자유도를 활용하지 못한다는 단점이 있다. (길이가 L인 codeword vector [x_1, x_2, ... ,x_L]에 대해 모든 성분이 동일하기 때문에 symbol의 degrees of freedom이 1임)
(참고)
BPSK to QPSK : exploting the degress of freedom (tistory.com)
이러한 문제를 해결하기 위한 여러가지 방법이 있고, 이 포스트에서는 그 중 하나인 Rotation Code에 대해 공부한다.
1. Rotation code
coherent 조건 하에서 2번의 time index에 걸쳐 symbol을 전송한다고 가정할때(즉 L=2) 다음의 벡터를 전송한다:

벡터 x의 두 가지 원소는 각각 독립적인 BPSK modulation을 사용하며, time diversity를 확보하기 위해 두 원소를 동일 시간에 전송하는 것이 아닌 두번의 time index (m=2)에 걸쳐 순서대로 전송한다. 따라서 총 4가지의 code를 사용할수 있고 아래와 같다:

Repitition code와의 비교를 위해, 동일한 time diversity L=2를 가지며 4개의 symbol을 전송할수 있는 code를 고려해보면 다음과 같고

동일한 경우에 Repitition code보다 Rotation code보다 (에너지 및 자유도 관점에서)더 나은 modulation 방법임을 확인할수 있다.
2. error probability
Rotation code의 정확한 에러 발생 확률을 구하는 것은 어렵기 때문에 확률의 union 개념을 사용하여 계산한다.(참고:Probability (tistory.com)의 7번)
1의 그림에서 보듯이 각 code들이 원점대칭이므로 편하게 x_A를 송신하였을때의 에러 발생 확률만 구해도 된다. 이때의 에러 발생 확률 p_e는 다음 부등식을 만족한다:
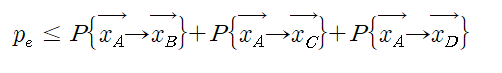
부등식의 우변을 계산하기 위해 시스템의 I/O 모델 및 Rayleigh fading 가정을 한다. I/O 관계식은 아래와 같고:

channel gain h_l이 Rayleigh fading을 따른다고 가정하면 첫 번째 확률을 구할 수 있다. 오직 두 개의 symbol만 존재하므로 이를 binary detection 이라고 생각하자. 전송신호 u_A, u_B는 아래와 같으며
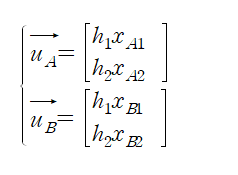
Appendix에서 배운 공식에 박으면 확률을 알 수 있다.
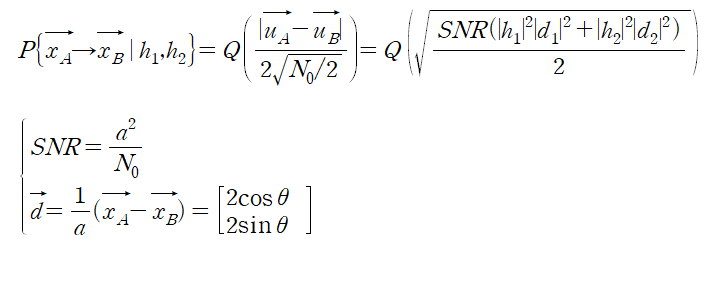
Q-function의 상계 Q<exp(-x^2 / 2), 를 사용하여 아래와 같이 부등식을 바꾸고:
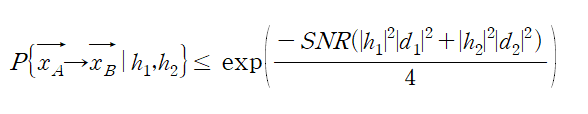
channel gain h의 분포를 알고 있으므로 부등식 우변에 평균값을 취해준다. 그렇게 하면 우변은 E[exp(sX)] 형태가 되는데, 이는 Random variable X의 MGF가 되므로, 지수분포를 따르는 |h|^2의 MGF에 값을 대입하는 방식으로 계산을 쉽게 할 수 있다.
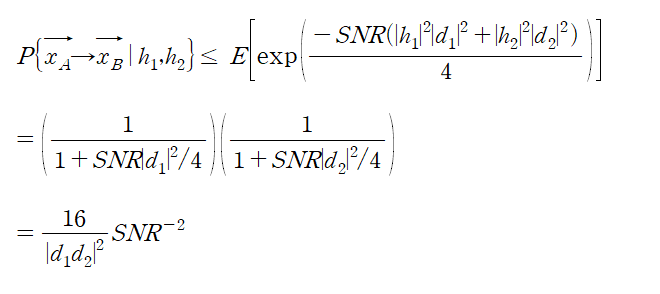
*마지막 식에서 SNR의 지수의 음수를 diversity gain 이라고 하며, |d_1 d_2|^2를 squared product distance라고 한다.
하여튼 이 결과를 가지고 전체 에러 발생 확률의 상계를 계산해보면
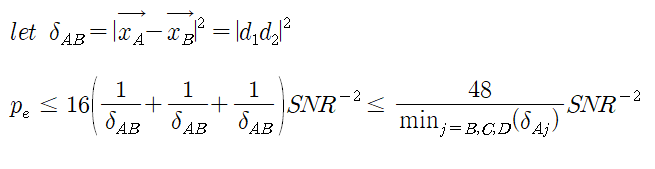
상계를 감소시키기 위해 각각의 squared product distance를 계산한다음 theta값을 최적화하면 다음과 같은 결론을 얻는다(귀찮으니까 계산생략).

3. Repetition code와의 비교:
그림

에서 Rotation code와 Repetition code의 성능 비교를 해보자.
첫번째로 Rotation code는 a^2 / N_0, Repetition code는 5a^2 / N_0(평균값) 의 SNR 값을 가진다. 따라서 에너지 관점에서 Rotation code가 더욱 효율적인 modulation 방법이다.
두번째로 에러 발생 확률을 비교하기 위해 Repetition code의 에러 발생 확률을 계산한다. union 개념은 항상 성립하므로 이를 통해 Repetition code의 에러 발생 확률을 계산하면 75SNR^-2의 상계를 가지게 되는데, Rotation code의 에러 발생 확률이 15SNR^-2 의 상계를 가지므로 에러 발생 측면에서도 더 높은 자유도를 가지는 Rotation code가 더 나은 성능을 가짐을 알수 있다.
'개인공부 > Wireless Comm.' 카테고리의 다른 글
| Antenna Diversity, MISO (0) | 2022.02.10 |
|---|---|
| Antenna Diversity, SIMO (0) | 2022.02.07 |
| Time Diversity, non coherent detection: Orthogonal modulation (0) | 2022.01.30 |
| Time Diversity, Coherent detection (0) | 2022.01.17 |
| BPSK to QPSK : exploting the degress of freedom (0) | 2022.01.13 |