지금까지 미분방정식을 푸는 방법에 대해 공부했고 주로 선형 미분방정식에 대해 다루었다. 영공간의 해를 지수함수 꼴이라 예측하고 풀었으며 입력이 지수함수 혹은 삼각함수(지수함수) 꼴일 때 또한 지수함수의 특성을 이용하여 풀었다.
지수함수의 특성을 사용하여 풀었다는 것이 무슨 말이냐.. 특성 방정식을 생각해 봤을 때 미분으로 이루어진 방정식에서 특성 방정식을 도출해내 미분방정식이 아닌 대수 방정식을 풀었고, 그로부터 미분방정식의 올바른 해를 얻었다. 적분인자 M(t)를 도입해 미적분 영역에서만 푸는 것보다는 특성 방정식을 도입해 대수 영역에서 푸는 것이 훨씬 빠르고 쉬웠다.
이 포스트에서 써놓은 라플라스 변환(laplace transform)은 선형 미분방정식을 대수 영역에서 푸는 체계적인 방법이다. 변환을 통해 얻은 해는 지금까지와는 달리 영공간의 해와 특수해로 이루어진 완전해이며 지수함수가 아닌 다항함수나 델타함수, 계단함수 등 모든 함수들에 대해서 사용이 가능한 방법이다.
미분방정식을 대수방정식으로 바꾸기
임의의 t에 대한 함수(미분방정식)를 라플라스 변환하게 되면 s에 대한 함수(대수방정식)로 바뀌게 된다. 모든 항을 변환하여 s에 대한 대수방정식을 만든 후 s로 표현된 해를 찾은 다음, 다시 t에 대한 함수로 역변환하면 처음에 얻고자 한 해 y(t) 를 얻는다.
예를 들어 모든 초기조건이 0인 방정식 d^2 y / dt^2 - 4dy/dt +3y = e^at 를 풀어보면 (2.7절 예제 1번)
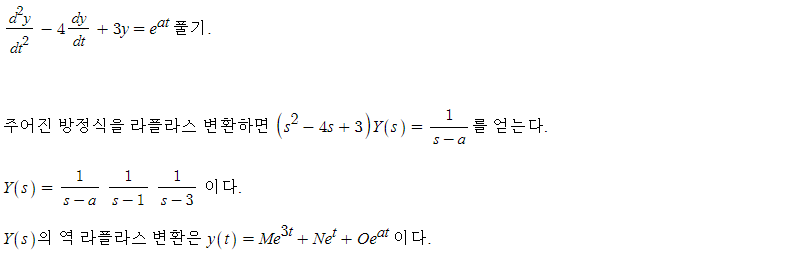
지금까지 지수함수를 이용해 풀었던 방법과 유사함을 확인할 수 있다. 이러한 과정을 일반화한것이 라플라스 변환이다.
1. 라플라스 변환
함수 f(t)의 라플라스 변환은 다음과 같다.

적분의 하한이 0 - ε 이라고 나와있긴 한데, 그냥 편하게 0으로 잡고 풀어도 된다. 이로인해 문제가 발생한다면 쉽게 알아차릴 것이므로 그때 다시 풀면 된다.
예시로 간단하게 e^at 의 라플라스 변환을 구해보면

s > a인 경우에만 변환이 s에 대한 함수로 수렴하는 것을 볼 수 있다. 이렇듯 라플라스 변환에서는 s > a 를 필요로 한다.
이를 더욱 일반적인 의미로 확장한다면 라플라스 변환의 피적분함수 f(t) 는 모든 t < 0 에 대해 f(t) = 0 즉 함수가 시작되지 않는다고 볼 수 있다.(시간이 진행되기 전에는 어떠한 입력도 없다, 혹은 f(t)H(t)로 볼 수도? 솔직히 뭔소린지 모르겠음)
또한 적분에서 분배법칙이 성립하므로 적분으로 정의되는 라플라스 변환 또한 분배법칙이 성립한다. 즉 F(f + g) = F(f) + F(g) 이다. (선형성)

다항함수, 삼각함수 등도 어렵지 않게 변환이 가능하다. 구글에 검색하면 나오니까 나중에 까먹으면 검색 ㄱ
2. 도함수 dy/dt 의 라플라스 변환
라플라스 변환을 사용하여 방정식을 풀 때 y(t) 를 미지의 변환 Y(s)라 두고 푸는 데 이때 y의 도함수 dy/dt 의 변환또한 필요하다. 공식에 그냥 박으면 답을 찾을수 있다.

이 기본적인 방법을 응용해 n차 도함수들의 라플라스 변환까지 구할 수 있다.
3. 라플라스 변환법으로 미분방정식의 완전해 구하기
이미 언급한 방정식 d^2 y / dt^2 - 4dy/dt +3y = e^at 을 직접 풀어보자. 초기조건 y(0) = 1, y'(0)=1 로 하자.

여기서 라플라스변환의 몇가지 성질을 알수 있다:
1. 라플라스 변환으로 구한 해 y(t) 는 영공간의 해와 특수해가 포함된 완전해이다.
최종 결과 y(t) 를 보면 지수함수 e^t, e^3t 가 포함되어 있음을 볼 수 있다. 이는 영공간의 해이고 e^at 부분은 특수해이다. 또한 각 계수 또한 식에 제대로 표현되어 있음을 알 수 있으며 t = 0 대입시 y(0)만 남게 된다.
2. 라플라스 변환은 공명의 경우또한 올바른 풀이법을 준다. (헷갈릴 일이 없다)
특성방정식 s^2 - 4s + 3 = 0의 해가 a값이 된다면 y(t)가 정의되지 않는다. 공명의 경우 해를 어떻게 구하는지는 다음 포스트에 설명한다.
3. y(t)의 라플라스 변환에 초기값을 반영하면 너무 복잡하다. 초기조건을 0으로 두고 푼 다음 마지막에 초기조건들을 맞춰주어도 된다.
모든 초기조건이 0이라면 n계 도함수의 라플라스 변환은 단지 Y(s)에 s를 n번 곱해준 것과 같다. 단순히 해의 형태만 알고 싶다면 이렇게 푸는 것이 나을수 있다.

'개인공부 > 미분방정식' 카테고리의 다른 글
| 라플라스 변환 기초(2) (0) | 2021.12.24 |
|---|---|
| 미정계수법과 매개변수 변환법 (0) | 2021.12.24 |
| n차 미분방정식의 특수해 구하기: 지수함수, 코사인함수 (0) | 2021.12.24 |
| n차 미분방정식의 영공간 해 구하기 (0) | 2021.12.24 |
| n차 미분방정식 풀이를 위한 성질들 (0) | 2021.12.24 |